スーパーコウルール下でのnコウの勝利判定

スーパーコウルールの下で画像のような局面での勝敗判定を行うロジックを紹介します。
なお、この記事の本線ではパスの考慮をしません。パスがある場合の結論も記載してますが、こちらは単純です。
前置き
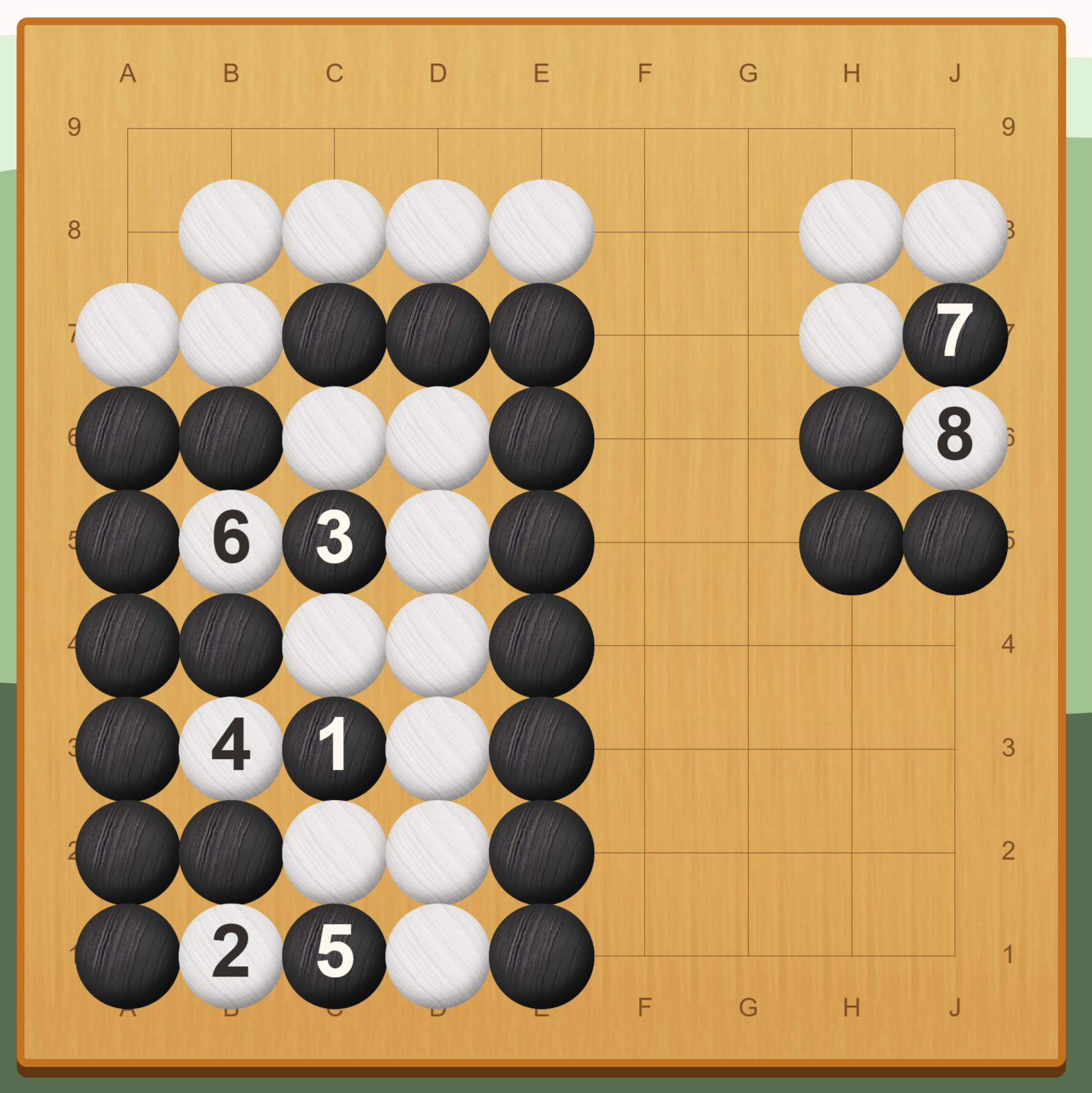
囲碁では特殊な条件下で無限ループに陥ります。
日本ルールではコウを除き無限ループに陥った場合引き分けになります。
一方、中国ルールなどではスーパーコウと呼ばれる反復盤面の禁止ルールがあり、無限ループが起きない仕組みになっています。
つまり、日本ルールでは無限ループで引き分けとなるケースであってもスーパーコウルール下では片方が必ず勝つことになります。
無限ループの一つであるnコウにおける勝利判定のロジックを考えてみたところ、興味深い結果になったので紹介するというのが本記事です。
盤面のモデル化
早速ですが、囲碁の盤面は情報量が多いので必要な情報だけ抽出します。
状態としては以下の3つを $(n, m, t)$ として管理します。
- $n$: コウの数
- $m$: 黒が取った形のコウの数
- $t$: 手番(0が黒番、1が白番)
例えば、例題の状態は $(50, 17, 0)$ です。
スーパーコウルールを適用するためには過去の盤面履歴が必要ですが、それを管理しないように次節の操作が設計されています。
モデルに行える操作
コウを中途半端にとった状態を考慮すると履歴管理が必要となるので、コウ争いなどを経て、どちらかが諦めてコウを埋める操作をした断面で状態を管理します。
パスを考慮していない点に注意してください。
- コウを埋める
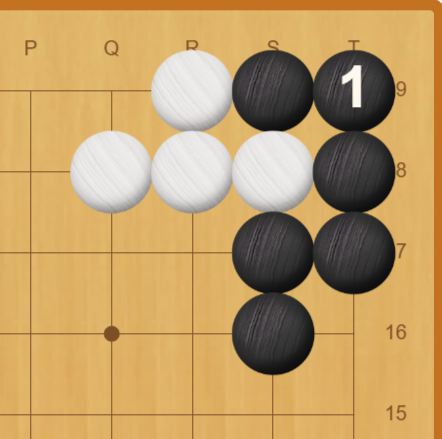
自分が埋める権利があるコウを1つ埋める操作です。
常に行える操作になります。
自分のコウを1つ減らして相手に手番を渡すので状態遷移は以下になります。
黒番のとき: $(n, m, t) \to (n-1, m-1, 1-t)$
白番のとき: $(n, m, t) \to (n-1, m, 1-t)$
- コウに勝ち、相手に埋めさせる
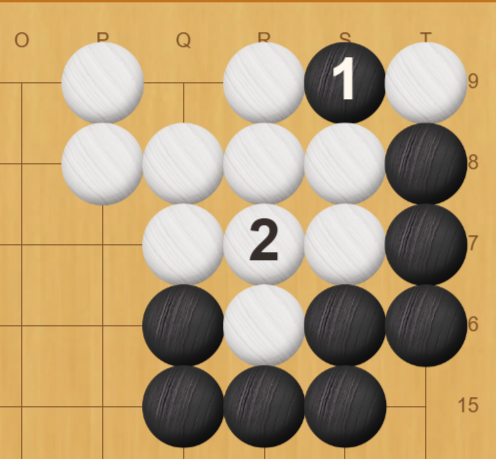
コウを取る操作を相手と繰り返し、スーパーコウルールにより相手にコウを埋めることを強制させる操作です。
こちらはコウ争い(ここでのコウ争いは囲碁でのコウ材などによるものではなく、同一盤面反復を回避する争いです)で相手に勝てる場合のみ行えます。
結論だけ先に言うと、自分の取っているコウが半分未満のとき(黒番だと $n \ge 2m+1$)にコウ争いに勝つことができます。
自分のコウを1つ増やして相手のコウを2つ減らし、また自分の手番になるので状態遷移は以下になります。
黒番のとき: $(n, m, t) \to (n-1, m+1, t)$
白番のとき: $(n, m, t) \to (n-1, m-2, t)$
コウ争いの勝敗判定
アルゴリズムに興味がある人向け節です。
初期状態 $(n, m, 0)$ のとき、コウ争いでは $n$ 個のコウのうち「$m$ 個を黒が取っている状態」と「$m+1$ 個を黒が取っている状態」を行き来することになります。
これは左に $\binom{n}{m}$ 個のノード、右に $\binom{n}{m+1}$ 個のノードを持つ2部グラフ上で互いに辺を選択することに対応します。
この時、頂点への再訪問が禁止の下で最期に辺を選択できなくなったほうが負けというゲームになります。
これは特殊な2部グラフ上での Vertex Generalized Geography と呼ばれる問題です。
本問題の場合では左右のうち頂点数が少ないほうを被覆する最大マッチングの存在が Hall の結婚定理からいえるため、ノード数が小さいほうが必ず勝つことが示せます。
なお、同数の場合は手番を持っているほうが勝ちます。
nコウの勝敗判定
状態に対して行える操作が定義されたので、理論的に閉形式を導出することも可能ですが、ここではまず実験的に解きます。
コウ争いの勝敗判定は上記のロジックでオラクルとした上で動的計画法で勝敗を表にしました。
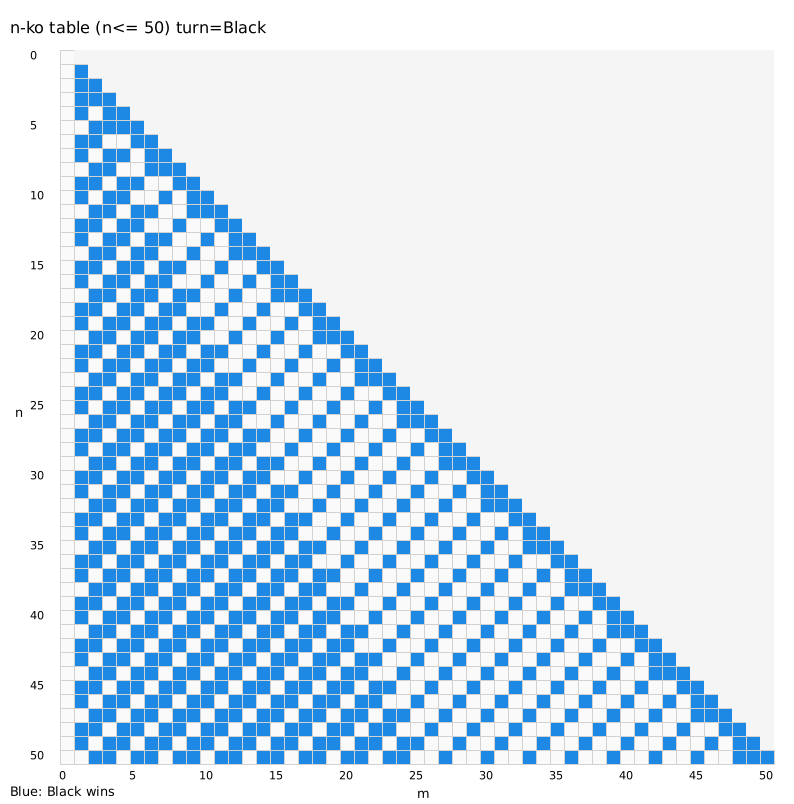
観察して整理すると、黒番の勝利条件は
- $m < n/2$ のとき: $(n+m) \bmod 3 \ne 1$
- $m \ge n/2$ のとき: $(n+m) \bmod 3 = 0$
となります。
言い換えると、
- 黒コウの数が白コウの数未満のとき、(コウの数+黒コウの数)を3で割ったあまりが1でないなら黒勝ち
- 黒コウの数が白コウの数以上のとき、(コウの数+黒コウの数)が3で割り切れるなら黒勝ち
となります。
なお、操作2が2手で1セットなことによる例外として、相手の石がアタリの時に手番が来たら即座に勝てます。
$(n, n-1, 0)$ と $(n, 1, 1)$ がそのケースです。
組合せゲーム理論的な直感
黒のコウの数 $m$ と白のコウの数 $(n-m)$ の差 $d=m-(n-m)=2m-n$ に注目します。
互いに操作1を行ったとき、互いのコウが1つ減り、差 $d$ は不変です。
また、自分の手番の時に手番を変えずに操作2を挿入することができる場合があります。
操作2を行ったとき、
黒番: $n \to n-1, m \to m+1$ より、 $2m-n$ は3増えます。
白番: $n \to n-1, m \to m-2$ より、 $2m-n$ は3減ります。
よって、操作2の挿入によって、$d$ は $\bmod 3$(3で割った余り)で不変だとわかります。
よって、黒番(もしくは白番)の時の $d \bmod 3$ は不変であることがわかります。
これらから、勝敗判定は $d \bmod 3$ 及び操作2が行えるか否かの境界 $m \ge 2n+1$ に依存して決まりそうだと予想できます。
この議論及び小さいケースでの結果をもとに議論を詰めると理論的にも導出できます(多分)。
例題の答え
本記事のタイトルの問題はコウが50個、黒のコウが17個で黒番なので状態は $(50, 17, 0)$ です。
$m < n/2$ であり、 $(n+m) \bmod 3 = 1$ より白勝ちの局面でした。
(おまけ)パスがある場合
パスによって盤面をそのまま相手に手番を渡す遷移ができるようになります。
連続でパスがされた場合は引き分けということにします。
このとき、黒番の勝利条件は $m >= n-1$ もしくは $(3, 1, 0)$ になります。
また、黒番の敗北条件はなく、勝利以外の場合は引き分けになります。
ラフには以下のような確かめられます。
$n=4$ で実験(シミュレーション)をすると $(4, 1, 0)$, $(4, 2, 0)$ が引き分けであり、勝利するには $(4, 3, 0)$ といった黒のコウの数が $m >= n-1$ になった状態を目指す必要があります。
しかし、コウの勝利条件の議論よりコウが多い側はコウを増やすことができないため、これは不可能であり、引き分けに落ち着くといった形になります。
よって、パスがある実際の囲碁的には、3コウは解決されますが4コウ以上は引き分けに落ち着きます。
おわりに
前の記事といい、囲碁周辺にはアルゴリズム的な話題が色々ありそうです。
組合せゲーム理論周りで囲碁関連の論文が色々出てるので紹介するのも面白いかもと思ってます。